Info

• Title: $\phi$-Decoding: Adaptive Foresight Sampling for Balanced Inference-Time Exploration and Exploitation
• Group: Shanghai AI Lab, HKU
• Keywords: foresight sampling, inference-time optimization, large language models
• Venue: Submission to ACL 2025

Challenge

The paper presents a novel inference-time optimization technique called “$\phi$-Decoding” for large language models (LLMs). The authors identify key challenges in auto-regressive LLM generation:

1. Short-sightedness of auto-regressive generation, which makes models unable to achieve global optima
2. Excessive exploration and insufficient exploitation in search-based methods
3. Inadequate step value estimation in existing approaches
4. Inefficient computational resource allocation (over-thinking issue)

Method

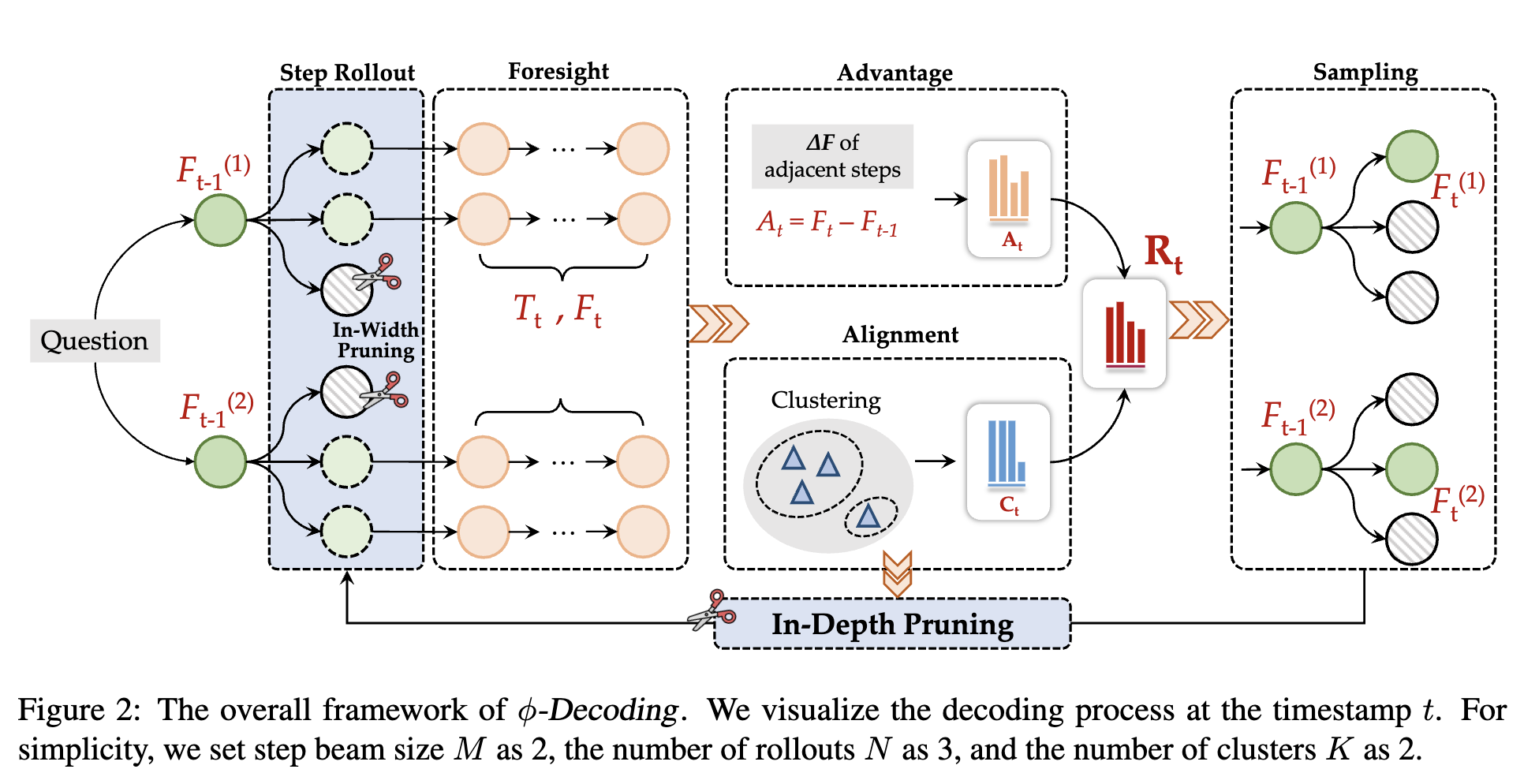
The authors introduce “$\phi$-Decoding,” a novel decoding strategy that frames the problem as “foresight sampling.” The approach:

1. Foresight Sampling: Uses simulated future steps to estimate globally optimal steps, conditioning generation on both preceding and future steps.

2. Step Value Estimation: Evaluates foresight paths using two distributions:

   • Advantage Estimation: Measures the improvement in probability between adjacent steps ($A_t = F_t - F_{t-1}$)
   • Alignment Assessment: Uses clustering to determine how consistent a step’s outcome is with other candidates

3. Dynamic Pruning Strategy: Optimizes computational resource allocation:

   • In-Width Pruning: Filters out low-confidence steps before foresight simulation
   • In-Depth Pruning: Implements early stopping when a large consensus emerges in foresight paths

The step value is computed by combining normalized advantage and alignment values, creating a joint distribution from which the optimal steps are sampled.

Results

The authors evaluated $\phi$-Decoding across seven reasoning benchmarks using various LLM backbones:

1. Performance Improvements:

   • Improved LLaMA3.1-8B-Instruct by 14.62% over auto-regressive CoT
   • Improved Mistral-v0.3-7B-Instruct by 6.92% over CoT
   • Consistently outperformed strong baselines including Tree-of-Thoughts, MCTS, Guided Decoding, and Predictive Decoding

2. Efficiency:

   • Achieved better performance with lower computational costs than baselines
   • 6× more efficient than suboptimal methods when targeting similar performance levels

3. Generalization and Scalability:

   • Worked effectively across LLM sizes ranging from 3B to 70B parameters
   • Successfully scaled to competition-level tasks like AIME 2024
   • Improved even the strongest reasoning LLMs (DeepSeek R1 models)

4. Ablation Studies:

   • Confirmed the value of foresight sampling (2.98%-6.09% gain)
   • Validated the contribution of clustering (0.95%-1.97% gain)
   • Demonstrated that dynamic pruning reduces computation while enhancing performance

Insights

1. Step Value Estimation: The accuracy of step value estimation correlates strongly with final answer correctness. By combining advantage and alignment distributions, $\phi$-Decoding achieves more accurate step value estimates than other methods.

2. Computational Efficiency: The dynamic pruning approach reveals that early reasoning steps are more critical and require more computational resources, while later steps can benefit from early stopping.

3. Generalization: $\phi$-Decoding’s effectiveness across model sizes (3B to 70B) suggests the approach addresses fundamental limitations in auto-regressive generation regardless of scale.

4. Adaptive Computation: The in-width and in-depth pruning strategies effectively allocate computational resources to challenging steps while conserving resources for simpler steps, alleviating the over-thinking issue.

5. Trade-offs: $\phi$-Decoding demonstrates a superior balance between exploration (finding diverse paths) and exploitation (focusing on promising paths), overcoming limitations of both search-based methods (excessive exploration) and auto-regressive methods (insufficient global awareness).

The paper makes a strong contribution by introducing an efficient, adaptive inference-time optimization algorithm that significantly improves LLM reasoning without requiring external models or additional training.

Comments

The method balances exploration and exploitation through two key components: (1) a step value estimation that combines “advantage” (measuring improvement from previous steps) and “alignment” (measuring consistency with other candidate paths through clustering) to create a joint distribution for optimal step selection, and (2) dynamic pruning strategies that include in-width pruning (filtering low-confidence candidates before expensive simulation) and in-depth pruning (implementing early stopping when consensus emerges).

Example

Consider a simple math problem where the LLM needs to generate a reasoning chain.

1. Foresight Sampling

Step t=1: The model needs to decide on the first reasoning step

Assuming M=2 (keep 2 candidate steps), N=2 (generate 2 possible next steps for each candidate)

The model generates 4 candidate first tokens/steps:

• Candidate A: [Token_A1, Token_A2, Token_A3]
• Candidate B: [Token_B1, Token_B2, Token_B3]
• Candidate C: [Token_C1, Token_C2, Token_C3]
• Candidate D: [Token_D1, Token_D2, Token_D3]

2. In-Width Pruning

Calculate the generation probability for these 4 candidates:

• A: 0.5
• B: 0.4
• C: 0.2
• D: 0.1

Calculate mean μ=0.3, standard deviation σ=0.16 Set pruning threshold at μ-σ = 0.14

Therefore, prune Candidate D (probability 0.1 < 0.14), keep A, B, C for foresight simulation.

3. Foresight Simulation and Step Value Assessment

For each retained candidate, the model performs foresight simulation to generate possible subsequent reasoning:

Candidate A foresight paths:

• Path A1: [Token_A1, Token_A2, Token_A3] → [Token_X1, Token_X2] → [Token_Y1, Token_Y2] → [Answer_1]
• Path A2: [Token_A1, Token_A2, Token_A3] → [Token_X3, Token_X4] → [Token_Y3, Token_Y4] → [Answer_1]

Candidate B foresight paths:

• Path B1: [Token_B1, Token_B2, Token_B3] → [Token_X1, Token_X2] → [Token_Y1, Token_Y2] → [Answer_1]
• Path B2: [Token_B1, Token_B2, Token_B3] → [Token_X5, Token_X6] → [Token_Y5, Token_Y6] → [Answer_2]

Candidate C foresight paths:

• Path C1: [Token_C1, Token_C2, Token_C3] → [Token_X7, Token_X8] → [Token_Y7, Token_Y8] → [Answer_3]
• Path C2: [Token_C1, Token_C2, Token_C3] → [Token_X9, Token_X10] → [Token_Y9, Token_Y10] → [Answer_2]

4. Calculate Step Values

Calculate Advantage:

• Calculate probability of each foresight path (averaged log probability)
• For Candidate A, assume combined foresight probability = 0.9
• For Candidate B, assume combined foresight probability = 0.88
• For Candidate C, assume combined foresight probability = 0.7
• Advantage values (compared to previous step) are A=0.9, B=0.88, C=0.7

Calculate Alignment:

• Cluster the foresight paths (based on token similarity)
• Find that most foresight paths lead to “Answer_1”
• Assume clusters for A, B, C have proportions 0.8, 0.5, 0.2 respectively
• Alignment values are A=0.8, B=0.5, C=0.2

5. Sample Optimal Steps

Combine Advantage and Alignment to compute the joint distribution:

• A: (normalized) advantage 0.36 + alignment 0.44 = 0.8
• B: (normalized) advantage 0.35 + alignment 0.28 = 0.63
• C: (normalized) advantage 0.29 + alignment 0.11 = 0.4

Sample from this distribution, likely selecting Candidates A and B as the two beams to continue reasoning.

6. In-Depth Pruning

As reasoning continues, if at some timestamp the largest cluster proportion exceeds a threshold (e.g., 0.7), then the foresight process can be terminated early, and the remaining steps completed using auto-regressive generation.

For example, at step 3, if 90% of foresight paths lead to the same answer [Answer_1], there’s no need to continue expensive foresight simulations, and the model can switch to regular auto-regressive generation to complete the final answer.

This example illustrates how $\phi$-Decoding uses foresight sampling to gain a more global perspective and dynamic pruning strategies to improve computational efficiency.