Info

• Title: Reconstruction vs. Generation: Taming Optimization Dilemma in Latent Diffusion Models
• Group: HUST
• Keywords: diffusion model, reconstruction, generation, optimization
• Venue: CVPR 2025

Challenge

The authors identify an “optimization dilemma” in latent diffusion models (LDMs):

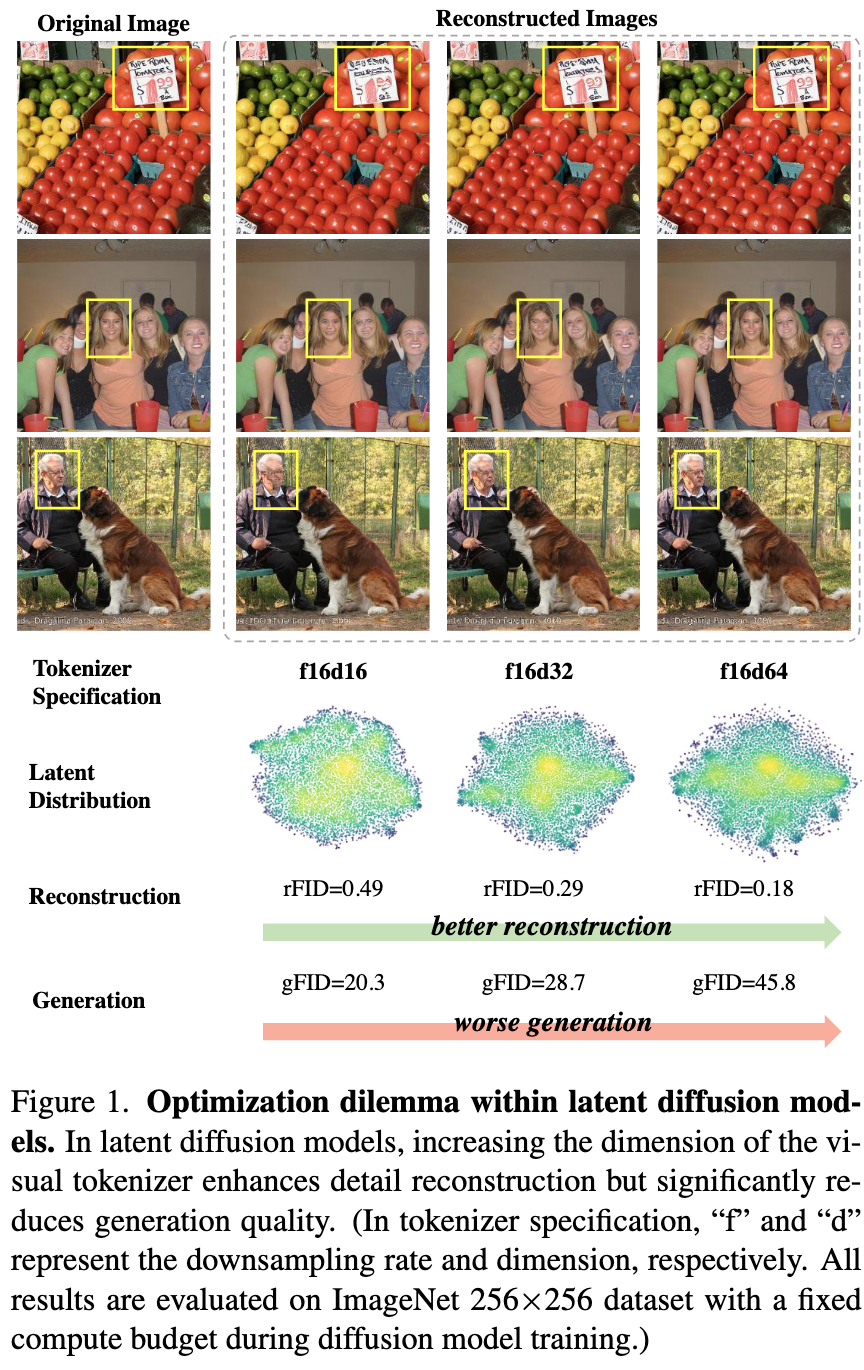
• Increasing the feature dimension in visual tokenizers (VAEs) improves reconstruction quality
• However, this leads to significantly worse generation performance
• Currently, researchers must choose between suboptimal solutions: either accept poor reconstruction with visual artifacts or deal with extremely expensive computation costs for training

This tradeoff creates a frontier where improving reconstruction typically worsens generation performance.

Method

To solve this dilemma, the authors propose:

1. VA-VAE (Vision foundation model Aligned Variational AutoEncoder): A novel approach that aligns the latent space of high-dimensional tokenizers with pre-trained vision foundation models

   • They introduce “VF Loss” (Vision Foundation model alignment Loss) which:
     • Uses marginal cosine similarity loss to enforce element-wise alignment
     • Uses marginal distance matrix similarity loss to maintain relative structures
     • Incorporates margins to prevent over-regularization

2. LightningDiT: An enhanced Diffusion Transformer with improved training strategies:

   • Advanced training techniques (Rectified Flow, logit normal sampling, velocity direction loss)
   • Architecture improvements (SwiGLU FFN, RMS Norm, Rotary Position Embeddings)

Results

The authors achieved remarkable improvements:

• State-of-the-art FID score of 1.35 on ImageNet 256×256 generation
• 21.8× faster convergence compared to the original DiT, reaching FID 2.11 in just 64 epochs
• Expanded the reconstruction-generation frontier, enabling high-dimensional tokenizers to maintain excellent reconstruction while also achieving superior generation performance
• 2.5-2.8× faster training with high-dimensional tokenizers

Insights

The key insight is that the optimization dilemma stems from the inherent difficulty in learning unconstrained high-dimensional latent spaces. When visualizing the latent space distributions:

• Higher-dimensional tokenizers learn latent representations in a less spread-out manner
• Vision foundation model alignment makes the distribution more uniform
• This uniformity appears correlated with better generative performance

The authors demonstrated that careful regularization of the latent space through alignment with vision foundation models can maintain the benefits of high-dimensional representation for reconstruction while making it more amenable to efficient generation, effectively resolving the tradeoff that previously limited latent diffusion models.

Comments

This paper elegantly resolves a fundamental dilemma in latent diffusion models where increasing feature dimensions improves reconstruction but degrades generation quality. The key insight is aligning VAE’s latent space with vision foundation models using a carefully designed Vision Foundation model alignment loss (VF Loss).

The VF Loss Design

The VF Loss consists of two complementary components:

1. Marginal Cosine Similarity Loss ($L_{mcos}$):

   $$L_{mcos} = \frac{1}{h \times w} \sum_{i=1}^{h} \sum_{j=1}^{w} \text{ReLU} (1 - m_1 - \frac{z^\prime_{ij} \cdot f_{ij}}{|z^\prime_{ij}| |f_{ij}|})$$

   This enforces element-wise similarity between the VAE’s latent features and vision foundation model features at each spatial location.

2. Marginal Distance Matrix Similarity Loss ($L_{\text{mdms}}$):

   $$L_{\text{mdms}} = \frac{1}{N^2} \sum_{i,j} \text{ReLU}\left(\left|\frac{z_i \cdot z_j}{|z_i| |z_j|} - \frac{f_i \cdot f_j}{|f_i| |f_j|}\right| - m_2\right)$$

   This preserves the relative spatial relationships between feature points across the entire feature map.

Both components include margin parameters ($m_1$ and $m_2$) to prevent over-regularization, allowing flexibility in the alignment.

The Adaptive Weighting Mechanism

The adaptive weighting mechanism brilliantly balances reconstruction and alignment objectives:

$$w_{\text{adaptive}} = \frac{|\nabla L_{\text{rec}}|}{|\nabla L_{\text{vf}}|}$$

The final VF loss is then applied as:

$$L_{\text{vf}} = w_{\text{hyper}} \cdot w_{\text{adaptive}} \cdot (L_{\text{mcos}} + L_{\text{mdms}})$$

This approach ensures neither loss dominates during training, creating more stable optimization without extensive hyperparameter tuning across different foundation models or tokenizer configurations.